¿Cuánto Mide el Diámetro de 10 cm?”

El diámetro de 10 cm es una medida importante en diferentes contextos. Antes de saber cuánto mide el diámetro, es esencial saber qué es el diámetro. El diámetro es la línea que atraviesa el centro de un círculo, y que une dos puntos de su circunferencia.

En el caso del diámetro de 10 cm, estamos hablando de una línea que mide exactamente 10 centímetros y que atraviesa el centro de un círculo de igual diámetro. Esto puede ser útil en la matemática, en la geometría y en la ingeniería. Por ejemplo, si se está diseñando una máquina con una rueda de 10 cm de diámetro, se debe saber que la línea que pasará por el centro de esa rueda mide exactamente 10 cm.

También resulta útil en la fabricación de objetos redondos, como tapas de recipientes, ruedas de bicicletas, entre otros. Para medir el diámetro de un círculo, se puede utilizar una regla o un calibre que permita medir en milímetros o en centímetros. Con estos instrumentos es posible saber si el diámetro es exactamente de 10 cm o si se encuentra ligeramente por encima o por debajo de esa medida.

En resumen, el diámetro de 10 cm es una medida importante en diferentes ámbitos y se refiere a una línea que atraviesa el centro de un círculo y mide exactamente 10 centímetros. Saber esta medida es útil en la matemática, en la geometría, en la ingeniería y en la fabricación de objetos redondos.

¿Cuál es el diámetro de 10 cm?

Para comprender correctamente la pregunta "¿Cuál es el diámetro de 10 cm?" es necesario tener claros algunos conceptos. En este caso, el diámetro es una medida que se utiliza para conocer la longitud de una línea que atraviesa el centro de una figura circular y que llega hasta sus bordes. Es una medida que se representa con la letra "d".

Al preguntar cuál es el diámetro de 10 cm, se está buscando conocer la longitud de la línea imaginaria que, partiendo del centro de un círculo, llega hasta sus bordes en una distancia de 10 centímetros. Esta medida es fácil de obtener, ya que una de las propiedades básicas de los círculos es que el diámetro es el doble de la longitud de su radio.

Por lo tanto, si se tiene un círculo de 10 cm de radio, su diámetro será igual a 20 cm. Esto se debe a que, al tratarse de una línea que parte del centro del círculo, su longitud es igual al doble de la distancia que existe entre el centro y sus bordes.

En resumen, si se desea conocer el diámetro de un círculo de 10 cm de radio, se debe calcular 2 veces esa medida, lo que resulta en un diámetro de 20 cm.

¿Cuál es el área de un círculo de 10 cm de diámetro?

El diámetro de un círculo es la distancia más larga que se encuentra en su interior, pasando por el centro. En este caso, el diámetro del círculo es de 10 cm, lo que significa que su radio es la mitad de esa medida, es decir 5 cm.

El área de un círculo se calcula multiplicando el valor de π (pi) por el radio del círculo al cuadrado. Si usamos el radio de 5 cm, tenemos:

Área del círculo = π x radio al cuadrado = π x 5 cm x 5 cm = 78.5 cm².

Así que, el área del círculo de 10 cm de diámetro es de 78.5 cm².

¿Cómo se mide el diámetro?

El diámetro es una medida geométrica fundamental que se define como la distancia más larga entre dos puntos opuestos de una circunferencia o de otra figura geométrica. Para medir el diámetro de un objeto, es necesario utilizar un instrumento de medición adecuado, como un calibre o una regla graduada.

La manera más precisa de medir el diámetro de una figura geométrica es utilizando un calibre digital. Este dispositivo permite medir hasta el último decimal, y tiene la capacidad de tomar medidas tanto internas como externas. Para medir el diámetro, el calibre debe colocarse correctamente y presionarse ligeramente para que se ajuste a la figura geométrica.

Otro método común para medir el diámetro es utilizando una regla graduada. Este método es menos preciso que el calibre digital, ya que la regla solo permite medir hasta la unidad más cercana. Para medir el diámetro con una regla graduada, se debe colocar la regla sobre el objeto, alineando el inicio de la regla con uno de los lados de la figura geométrica. Luego, se debe leer la medida en la unidad más cercana.

En conclusión, medir el diámetro es una tarea sencilla y fundamental para identificar las propiedades geométricas de los objetos. Para esto, existen distintos instrumentos de medición que pueden ser utilizados, desde los más precisos como el calibre digital, hasta los más simples como la regla graduada. Es importante utilizar el instrumento de medición correcto para garantizar medidas precisas y obtener resultados confiables.

¿Cómo calcular la longitud de una circunferencia de 10 cm de diámetro?

Calcular la longitud de una circunferencia es sencillo si se conocen las medidas necesarias. En este caso, tenemos un diámetro de 10 cm, por lo que el primer paso es encontrar el radio de la circunferencia.

Para ello, se divide el diámetro entre dos y se obtiene un radio de 5 cm. A partir de aquí, se aplica la fórmula matemática para calcular la longitud de una circunferencia: L = 2πr, siendo "r" el radio de la circunferencia y "π" una constante matemática.

Sustituyendo los valores, L = 2π(5 cm) = 10π cm. Esta sería la longitud de la circunferencia si el radio es de 5 cm y el diámetro de 10 cm.

Es importante conocer esta fórmula, ya que puede ser muy útil en distintas situaciones, como por ejemplo para calcular el tamaño o el perímetro de círculos en objetos o estructuras, ya sean ruedas, piscinas, edificios y un sinfín de otros ejemplos.

Reglas de medición

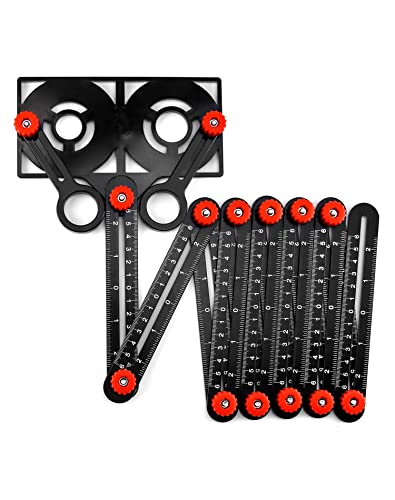
QWORK® Regla de Medición de Múltiples Ángulos, 12 Laterales Rgla Plegable Herramienta de Plantilla con Orificio de Posicionamiento, Ideal para Artesano,Carpintero,Arquitecto

• Material de primera calidad: hecho de aleación de aluminio de 3,6 mm de espesor, anticaída, duradero, no es fácil de usar y rasgar.
• Medición precisa: unidades métricas e imperiales, con una precisión de 1 mm.
• 12 lados: 12 reglas y 12 perillas de metal que se pliegan libremente. Simplemente ajuste las perillas de metal para crear con precisión la forma que desee.
• Localizador de apertura de 5 tamaños: 20 mm, 25 mm, 40 mm, 45 mm y 80 mm. Super flexible y versátil.
• Amplia aplicación: adecuado para trabajos de carpintería, ladrillo, baldosas de cerámica, madera, vidrio, piedra, laminado, proyectos de construcción e ingeniería.

Ver precios en

Regla de Medición Herramienta de Plantilla - 12 Lados Aleación de Aluminio Plegable Multi Angulo Regla de Medidas para Artesano, Constructor, Arquitecto Negro

• Regla de Medición Multifuncional: no solo es una herramienta de medición de múltiples ángulos, sino también una regla de plantilla con sierra de perforación para colocar baldosas. 12 reglas individuales se pueden montar y desmontar rápidamente para lograr la forma deseada.
• Material Premium: la regla de medición multiángulo está hecha de aleación de aluminio súper duradera. ¡Tornillos incluidos! Son más resistentes que los botones de plástico y, por lo tanto, más duraderos. L'attrito tra i metalli può causare graffi, ma non ne pregiudica l'uso.
• Fácil de Usar: apriete la tuerca para asegurar, medir y ajustar completamente el ángulo. Se puede plegar y guardar fácilmente para ahorrar espacio. Gracias a su diseño compacto, se puede transportar fácilmente a cualquier obra.
• Mediciones Precisas: nuestros medidores de ángulo son ideales para la medición precisa de ángulos. El cuerpo de la regla está impreso con dos unidades de medida: pulgadas y centímetros. Escalas impresas con láser para mantenerlas legibles para mediciones precisas durante largos períodos de tiempo.
• Amplia Aplicación: la regla de ángulo puede crear diseños de múltiples ángulos en segundos y se puede usar para medir y marcar en azulejos, piedra, madera y otros materiales. Si encuentra algún problema con el producto que recibió, no dude en contactarnos. Te lo resolveremos lo antes posible.

Ver precios en

Regla de medición multiángulo y de estilo lateral para azulejos de cerámica, 12 herramientas de ángulo de aleación de aluminio para arquitectos

• ❤ [Última versión] Con la herramienta angular de 6 piezas, puedes ajustar la posición de perforación a B. Marque las baldosas con precisión. Es una herramienta de medición y un posicionamiento de agujeros integrado. Esta regla de medición se pliega fácilmente y se guarda para ahorrar espacio y se puede llevar fácilmente a cualquier sitio de construcción. Es muy adecuado para medir la superficie de ladrillos, papel, piedra, baldosas de cerámica, madera y otros materiales.
• ❤ [Mejoras de materiales y diseño] La regla de medición multifunción está hecha de aleación de aluminio de alta calidad, superresistente al desgaste. Equipado con botones de metal. Son más fuertes que los botones de plástico y, por lo tanto, más duraderos. Los bordes son redondos y lisos, sin rebabas que pueden evitar lesiones. Sin procesamiento complicado.
• ❤ [Medición precisa] Nuestra regla de medición multiángulo es un instrumento ideal para medir ángulos precisos. Hay pulgadas y centímetros en la escala, todos los grabados láser no se desvanecerán ni desgastarán, incluso si usa la regla deslizante durante mucho tiempo, manténgala clara y fácil de leer para una medición precisa.
• ❤ [Fácil de usar] Simplemente coloque la herramienta de medición de ángulo en su área de trabajo, deslice la herramienta de medición de ángulo en la forma deseada y apriete los tornillos. La regla multiángulo se puede colocar en cualquier posición y fijar en cuestión de segundos para crear su propia plantilla. Además, los tornillos incluidos son grandes y se pueden reemplazar con una mano, lo que lo hace muy fácil de usar.
• ❤ [Amplia aplicación] La regla multiángulo de 6 lados es una herramienta universal de medición multiángulo que suministra artículos de ladrillo, madera, baldosas, pisos, techos y metal. Puede elegir un cuadrado de metal como regalo para constructores, solteros, carpinteros, artesanos, techadores, carpinteros, arquitectos, bricolaje, etc.

Ver precios en

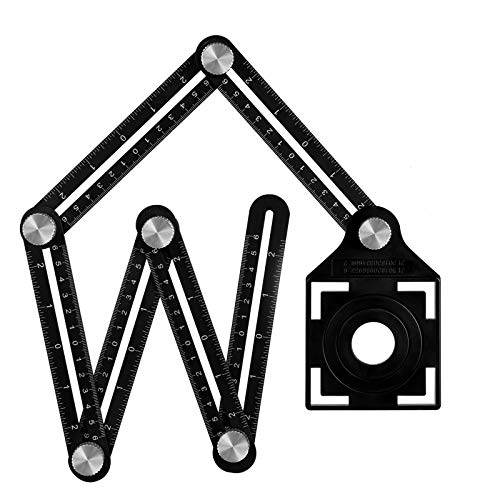
Regla de Medición Herramienta de Plantilla, Plegable Multi Angulo Regla de Medidas para Artesano, Constructor, Carpintero, Arquitecto【Aleación de Aluminio】

• 📏【Versión más reciente】 Con la herramienta de ángulo de 6 piezas puede ajustar la posición de taladrado a Z. Por ejemplo, marcar azulejos con precisión. Es una herramienta de medición y un posicionamiento de orificio integrado. Esta escuadra regla de medición se puede plegar y guardar fácilmente para ahorrar espacio. Debido a su diseño compacto, se puede transportar fácilmente a cualquier sitio de construcción. Ideal para medir la superficie de ladrillos, papel, piedra, azulejos y madera, ect.
• 📏【Diseño y material mejorado】 La regla de medición multifuncional hecha de una aleación de aluminio ultra resistente de alta calidad. Equipado con botones metálicos. Estos son mucho más robustos que los botones de plástico y, por lo tanto, más duraderos. Los transportador de angulos carpinteria tiene bordes redondos y lisos para evitar lesiones.
• 📏【Medición precisa】 Nuestra regla de medición de múltiples ángulos es el instrumento ideal para mediciones de ángulo precisas. La escala de regla tiene pulgadas y centímetros de impronta. 12 cm / 4 pulgadas. Todo el grabado láser no se desvanece y se desgasta. Adecuado para trabajadores de la construcción, artesanos y mejoras para el hogar. Una herramienta de medición indispensable y práctica en la caja de herramientas.
• 📏【Fácil de usar】 Solo coloque en su área de trabajo, deslice la transportador de angulos carpinteria en la forma que desee y apriete los tornillos. La regla de múltiples ángulos puede colocarse en cualquier posición y fijarse en segundos para crear su propia plantilla.
• ⚠⚠ Confirme la tienda "Wohao" antes de comprar. ☛ 【Servicio 100%】Si tiene algún problema con nuestro producto o no está satisfecho, contactanos, recibirá un reemplazo y una garantía de reembolso.

Ver precios en

calibradores

Vinabo Calibre Digital, Pie de Rey Clásico de 150 mm / 6 Pulgadas Inoxitable Calibrador con Pantalla LCD Grande Calibre para Mediciones Externas, Internas, de Profundidad y de Paso

• 📏【Material】 Calibre digital de acero inoxidable finamente pulido con rodillo moleteado y tornillo de bloqueo para garantizar la suavidad y precisión de la posición durante el uso. Con proceso endurecido, no se oxida, más duradero, más duradero. Estos calibres profesionales están pulidos y no cortan personas ni objetos.
• 📏【Precisión de la medición】El calibrador digital profesional viene con una pantalla LCD para ayudarlo a obtener resultados rápidamente. Rango de medición del calibre: 0 - 6" / 0 - 150 mm; Resolución: 0,01" / 0,1 mm; Precisión: ±0,02 mm/0,001" (100-200 mm). Tenga en cuenta que el micrómetro de precisión no es a prueba de polvo, aceite y agua, pero es a prueba de salpicaduras. Trate de evitar que el agua, la electricidad y el magnetismo afecten el producto.
• 📏 【Pantalla LCD extra grande】 Calibre analógico de una gran pantalla LCD fácil de leer que hace que la lectura de los resultados sea más clara. Y con la conversión instantánea de pulgadas/milímetros con solo tocar un botón, las lecturas se pueden mostrar en pulgadas o milímetros. La tecla cero le permite establecer el punto cero en cualquier lugar del calibrador y comenzar una nueva medición.
• 📏 【 Calibradores digitales versátiles 】 Los calibradores digitales convencionales pueden medir con facilidad y precisión el diámetro externo, el diámetro interior y la profundidad. Es una herramienta adecuada para la vida diaria, muy utilizada en familias, talleres y fábricas.
• 📏【Contenido del paquete】Calibrador digital, una batería de repuesto LR44 adicional de 1,5 V y una batería de calibre integrada, manual.

Ver precios en

Pie de Rey - 6 Pulgadas 150mm Calibre Analogico Calibrador Vernier Profesional Precision Calibre Pie de Rey para Medición Diámetro Profundidad

• Alta calidad: Acero de alto carbono, dispositivo de medición de alta calidad. Alta precisión: la precisión es de 0,02 mm / 0,001 pulgadas (menos de 100 mm) y 0,03 mm / 0,001 pulgadas (100 - 150 mm)
• Duradero y duradero: Material de acero con alto contenido en carbono y no necesita batería. Una herramienta ideal para uso de por vida
• Multifunción: la pinza métrica es de 0 a 6 pulgadas / 150 mm, puede medir el diámetro exterior, el diámetro interior, la profundidad y el valor de paso de un artículo exquisito, una herramienta multifuncional para ti. Rango de medición: 0 a 150 mm (0 a 6 pulgadas)
• El deslizamiento es suave, sin arena. Barra de profundidad integrada
• Superficie altamente pulida, peso pesado, diseño resistente con superficies de medición de Acero al carbono endurecido

Ver precios en

Pie de Rey Digital, LOUISWARE 150 mm /6 Pulgadas de Calibre Digital Electrónica, Paquimetro Profesional de Acero Inoxidable, Gran Pantalla Lcd, Durable, Medir Diámetro Interno, Diámetros y Profundidad

• 【Rango de medición】 0-150 mm( 6"), Precisión: ±0.02 mm (0.001"), calibre digital profesionales, Es preciso a la hora de medir con dos decimales de precisión【Rango de medición】 0-150 mm( 6"), Precisión: ±0.02 mm (0.001"), calibre digital profesionales, Es preciso a la hora de medir con dos decimales de precisión
• 【4 funciones de medición para mediciones flexibles】 Vernier Electronico Digital profesional mida el interior, el exterior, la profundidad y el paso con dos juegos de mordazas y la sonda. Perfecto para medir objetos pequeños; profundidades de agujeros, diámetros de objetos redondos
• 【Pantalla digital de pantalla grande, lecturas claras】 Pantalla grande, lectura fácil en cualquier entorno, la escala y al instante Convierte entre Pulgadas/Milímetro con solo tocar un botón, Puesta a cero en cualquier momento ( velocidad de medición: ≤1.5 m/s)
• 【Acero inoxidable de alta calidad】 Calibrador digital electrónico de acero inoxidable pulido fino con ruedas moleteadas y tuerca de bloqueo para garantizar un posicionamiento suave y preciso durante el uso. Proceso de endurecimiento para que no se oxide, mayor durabilidad y vida útil
• 【Paquete incluye】 En la caja cabe el calibre digital, la pila de repuesto, el destornillador que se debe usar para cambiar la pila y el manual

Ver precios en

Newaner Calibre Digital, Pie de Rey de Fibra de Carbono de 150 mm / 6 " con Pantalla LCD Transparente y Batería de Respaldo, Calibre para Mediciones Externas, Internas, de Profundidad y de Paso

• 【Calibrador Digital Profesional】El pie de rey digital ha pasado nuestras rigurosas pruebas para garantizar una precisión más precisa. El rango de medición de los pie de rey digital es de 0 a 6 "/ 150 mm, lo que es muy adecuado para uso en el hogar, la escuela, el taller y la fábrica.
• 【Función Cero】El calibre digital profesional ​tiene un botón CERO, podemos restablecer el valor de medición, lo que hace que la operación de medición sea más flexible.
• 【Gran Pantalla LCD】Pantalla LCD grande y fácil de leer, la lectura se puede mostrar en formato de pulgadas o milímetros, la lectura es más clara, muy adecuada para personas con baja visión. Cuando no ha utilizado la calibrador digital mucho tiempo, la pcalibrador digitalse apagará automáticamente.
• 【Ligero y Portátil】La calibrador está hecha de material compuesto de fibra de carbono, que es más ligero y seguro que el acero inoxidable.
• 【Lo Que Puedes Conseguir】Calibre* 1, batería * 2 (el calibre puede durar más), caja de plástico * 1 (conveniente para almacenar y proteger el calibre)

Ver precios en

Aparatos de medición

Artibetter Medida del Pie De Los Niños Herramientas para Niños Dispositivo Brannock Aparatos para Medir Tallas De Zapatos Medición del Pie del Bebé Devices Niño Pequeño Pies Mesa De Medición

• regla de pie para niños: puede ayudarlo a medir los pies del bebé, compre el tamaño correcto de zapatos.
• Medición de pies para niños: dispositivo de medición de pies para niños, herramienta de medición de longitud de pie de bebé, regla de pie para niños, tamaño de zapato, kits de dispositivo de calibre de longitud de pie
• Dispositivos de medición de zapatos: ¡excelentes para pedir zapatos en línea o medir el tamaño de su familia antes de ir a la tienda!
• Medición del tamaño del zapato para niños: fácil de llevar a cualquier lugar, en cualquier momento que se te ocurra. Mediciones fáciles de usar y precisas.
• Medidor de pie de bebé: fantástica herramienta de medición para elegir los zapatos adecuados.

Ver precios en

Batería para Aparatos de Medicióne Stonex Modelo BT-L74SA

• La batería en detalle: ▶ Tensión: 7,4V | ▶ Capacidad: 2600mAh/19,2Wh | ▶ Modelo: Li-Ion | ▶ Medidas: 70,5mm x 38,5mm x 20,5mm | ▶ 100% compatible |
• Batería de reemplazo o repuesto para tu equipo de medida. Control de calidad: cada batería ha superado las más rigurosas pruebas de control de calidad antes de salir de fábrica.
• Argumentos por los que elegir esta batería de reemplazo: No tienes que comprar un nuevo aparato más costoso. De esta manera ahorras dinero mientras que ayudas a proteger el medio ambiente. Además, por lo general la sustitución de la batería es un proceso fácil y rápido.
• Producto de alta calidad y seguro. Electrónica de protección contra sobrecargas, contra sobretensiones y contra cortocircuitos. La nueva batería sirve para el cargador anterior del equipo. Sin efecto memoria gracias al empleo de la última tecnología.
• Más de 25 años de experiencia en el sector de la electrónica. Nuestro avanzado sistema de logística nos permite ofrecer la mayor disponibilidad de baterías con la fecha de fabricación más reciente, junto con una excelente relación precio / rendimiento. Además, como uno de los mayores importadores directos españoles de baterías, pilas y cargadores, Bateria_es te ofrece servicio y garantía española. Todo ello nos permite mantener la más alta satisfacción entre los usuarios de nuestros productos.

Ver precios en

Aparatos de medición

• Informativo
• Interesante
• Convenientemente

Ver precios en

OCS.tec 6-IN-1 Multi Meter Tester EC CF TDS PH °C °F REDOX Aparato MEDICION Medida P28

Ver precios en