Calcular el Volumen: Ejemplos Prácticos

El cálculo del volumen es una habilidad matemática importante que se aplica en diversos contextos, desde la física hasta la arquitectura. Saber cómo calcular el volumen de diferentes objetos puede ser útil en muchos aspectos de la vida cotidiana.

Un ejemplo práctico de cálculo de volumen es al calcular el volumen de un cubo. Para hacer esto, se debe multiplicar la longitud de un lado del cubo por sí misma tres veces, es decir, al cubo. Por ejemplo, si el lado de un cubo mide 5 cm, el volumen del cubo será de 125 cm³.

Otro ejemplo práctico es el cálculo del volumen de una esfera. La fórmula para calcular el volumen de una esfera es (4/3) π r³, donde r es el radio de la esfera. Si el radio de una esfera es de 2 cm, el volumen de la esfera será de 33.52 cm³.

Un tercer ejemplo práctico es el cálculo del volumen de un cilindro. La fórmula para calcular el volumen de un cilindro es π r² h, donde r es el radio de la base del cilindro y h es la altura del cilindro. Si el radio de un cilindro es de 3 cm y su altura es de 6 cm, el volumen del cilindro será de 169.65 cm³.

El cálculo del volumen también se puede aplicar a objetos más complejos, como una piscina de forma irregular. En este caso, se pueden utilizar diferentes métodos, como dividir la piscina en secciones y calcular el volumen de cada sección por separado, para luego sumar los volúmenes obtenidos. Este tipo de cálculos pueden resultar más complicados, pero siguen los mismos principios básicos.

En resumen, el cálculo del volumen es una habilidad matemática útil en muchos aspectos de la vida cotidiana. Entender cómo calcular el volumen de diferentes objetos puede ayudar en diversas situaciones, desde determinar la cantidad de líquido que cabe en un recipiente hasta planificar la construcción de un edificio. Es importante practicar y comprender las fórmulas y conceptos básicos para poder aplicar el cálculo del volumen de manera efectiva.

¿Cómo se puede calcular el volumen?

El cálculo del volumen es una operación matemática que permite determinar el espacio ocupado por un objeto o una sustancia. Es una medida tridimensional que se expresa en unidades cúbicas.

Existen diferentes fórmulas para calcular el volumen, en función de la forma del objeto o sustancia. Por ejemplo, el volumen de un prisma rectangular se calcula multiplicando el área de la base por la altura.

Otras figuras geométricas, como por ejemplo el cilindro, el cono o la esfera, tienen fórmulas específicas para calcular su volumen.

Una regla básica para el cálculo del volumen es que todas las dimensiones deben estar en la misma unidad de medida. Por ejemplo, si se trabaja con centímetros cúbicos, tanto el largo, el ancho como la altura deben estar en centímetros.

Es importante destacar que para objetos irregulares, el cálculo del volumen se puede realizar mediante la técnica del desplazamiento de agua. En este caso, se sumerge el objeto en un recipiente con agua y se mide la cantidad de agua desplazada.

En resumen, el cálculo del volumen es una herramienta matemática fundamental en diferentes áreas, como la física, la química o la geometría. Conocer cómo calcular el volumen de distintos objetos o sustancias nos permite comprender mejor su comportamiento y propiedades.

¿Cómo se calcula el volumen en litros?

El volumen es una magnitud que se utiliza para medir el espacio ocupado por un objeto o sustancia en tres dimensiones. En el sistema métrico, el volumen se expresa comúnmente en litros.

Para calcular el volumen en litros, se debe conocer previamente las dimensiones del objeto o sustancia en cuestión. Generalmente se mide el ancho, el largo y la altura del objeto.

Una vez que se conocen las dimensiones, se realiza una simple operación matemática para obtener el volumen en litros. La fórmula general para calcular el volumen de un objeto rectangular es:

Volumen (en litros) = Largo x Ancho x Altura

Es importante asegurarse de tener las dimensiones en la misma unidad de medida para realizar el cálculo correctamente. Si las dimensiones se encuentran en diferentes unidades, es necesario convertirlas a la misma unidad antes de realizar la operación.

Por ejemplo, si se quiere calcular el volumen de una caja rectangular cuyas dimensiones son 20 centímetros de largo, 15 centímetros de ancho y 10 centímetros de altura, se realizaría el cálculo de la siguiente manera:

Volumen (en litros) = 20 cm x 15 cm x 10 cm = 3000 cm³

En este caso, el resultado obtenido es en centímetros cúbicos. Para convertirlo a litros, se debe recordar que 1 litro equivale a 1000 centímetros cúbicos. Por lo tanto, el volumen en litros sería:

Volumen (en litros) = 3000 cm³ / 1000 = 3 litros

Así, el volumen de la caja rectangular sería de 3 litros.

¿Qué es el volumen y cómo se mide?

El volumen es una magnitud física que se utiliza para medir el espacio ocupado por un objeto o substancia. Se refiere a la cantidad de espacio tridimensional que ocupa un objeto o la capacidad de un recipiente.

En física, el volumen se mide en metros cúbicos (m³) o en las unidades cúbicas correspondientes al sistema utilizado, como centímetros cúbicos (cm³) o litros (L).

Existen diferentes métodos para medir el volumen, dependiendo de la forma y la naturaleza del objeto a medir. Un método común es utilizar una regla o cinta métrica para medir las dimensiones del objeto en tres dimensiones: largo, ancho y alto. Luego, se multiplican estas dimensiones para obtener el volumen.

Para objetos regulares, como un cubo o una esfera, existen fórmulas matemáticas específicas para calcular el volumen. Por ejemplo, el volumen de un cubo se obtiene multiplicando la longitud de uno de sus lados por sí mismo tres veces: V = lado x lado x lado.

En el caso de líquidos, se utiliza un instrumento llamado probeta para medir el volumen. La probeta es un tubo de vidrio graduado que permite medir de manera precisa la cantidad de líquido que se inserta en ella.

En resumen, el volumen es una medida que nos permite determinar el espacio tridimensional que ocupa un objeto o la capacidad de un recipiente. Se puede medir utilizando diferentes técnicas y unidades de medida, como métodos directos o fórmulas matemáticas específicas.

básculas digitales

Rowenta BS1400 Premiss - Báscula de baño con Pantalla LCD, de diseño fino de 2cm de alto, hasta 150 kg y 100 gr de precisión, encendido y apagado automático, Negro

• Báscula de baño con superficie de vidrio con pantalla digital amplia con dígitos de fácil lectura de 23 mm de alto
• Estructura extraplana de solo 2cm de alto y base de cristal templado de 30x30 cm; material de la superficie fácil de limpiar
• Conexión automática: La báscula se enciende automáticamente al subirse y a los 5 segundos de bajarse de ella
• Peso máximo hasta 150 kg con una sensibilidad de 100 gr de graduación
• Funciona con una pila CR2032, incluída en el producto para un uso inmediato de la báscula
• Gran comodidad de uso, precisión y diseño
• Las dimensiones de la báscula son de 30 x 30 x 2 cm

Ver precios en

RENPHO Bascula de baño electrónica, Báscula digital de alta precisión con pantalla LED, de diseño fino, peso máximo de 180 kg y 50 gr de precisión, Negro

• Las bascula de baño son siempre precisas: Sensores de alta precisión trabajan en tándem para proporcionarle mediciones exactas en las que puede confiar, hasta 0,05kg/0,1lb. La bascula tiene una capacidad máxima de peso de 180kg/400lbs.(2 pilas AAA incluidas).
• Tecnología paso a paso: Esta báscula digital utiliza tecnología paso a paso avanzada, por lo que todo lo que tiene que hacer es subirse a la plataforma de calibración automática. En cuestión de segundos, recibirá mediciones de peso precisas, instantáneas y consistentes en kilogramos o libras. Despídase de las esperas.
• Fácil de usar: La bascula baño está equipada con una pantalla LCD ultrabrillante que facilita la visualización de los números en todas las condiciones y mantiene el mismo brillo durante el ciclo de vida de la batería. La bascula de baño dispone de encendido/apagado automático, calibración automática, indicador de batería baja e indicador de sobrecarga. Dispone de dos unidades de medida (lbs/kg).
• Redondeada y suave, segura y fiable: Esta báscula electrónica está diseñada con esquinas redondeadas para evitar bordes afilados y garantizar la seguridad de todos los miembros de la familia. Equipada con un marco de soporte y almohadillas antideslizantes para evitar resbalones. La construcción de vidrio templado de 5 mm es resistente y duradera, y la superficie lisa es fácil de limpiar y mantener.
• Tamaño compacto: El diseño sencillo y estilizado es fácil de guardar y utilizar en cualquier lugar. Toda la plataforma está acabada en negro clásico, que complementa incluso los cuartos de baño más elegantes. (Las dimensiones de la báscula son de 26 x 26 x 2.2 cm)

Ver precios en

RENPHO Bascula de Baño Digital Grasa Corporal, Balanza Bluetooth Inteligente con App, Bascula Electrónica Analógica con Análisis Corporal, 13 Medicióne de Peso IMC Visceral e Muscular, Elis 1

• La aplicación inteligente se sincroniza con la aplicación de fitness - millones de usuarios felices en todo el mundo. La aplicación Renpho Health funciona con Samsung Health, Apple Health, Fitbit, Google Fit. La aplicación también está disponible para Apple Watch.
• Análisis de 13 datos de composición corporal - salud, incluido el peso, el IMC, la grasa corporal, peso libre de grasa, grasa subcutánea, grasa visceral, agua corporal, músculo esquelético, masa muscular, masa ósea, proteína, TMB y edad metabólica.
• Guardar y compartir - guarde sus medidas y controle su salud. Puedes seguir la evolución de tu condición física o descargar datos gracias al gráfico generado. También puede compartir sus datos de fitness con su familia y amigos.
• Alta precisión y alta calidad - con tecnología "step-on" y una plataforma de vidrio templado de 5 mm de alta calidad, en incrementos de 0,2 lb / 0,05 kg con una capacidad máxima de 400 lb / 180 kg / 28. 4 sensores de alta precisión garantizan mediciones precisas. Las funciones de autocalibración y apagado automático brindan una mayor duración de la batería.
• Una escala para un número ilimitado de usuarios - puede crear un número ilimitado de cuentas en la aplicación Renpho Health, donde puede guardar todos los datos de todos los miembros de la familia. También es compatible con el modo bebé que puede registrar el peso de niños y mascotas. La aplicación funciona con Bluetooth 4.0 o superior. Puede pesarse en cualquier momento sin su dispositivo móvil, los datos se sincronizarán con la aplicación una vez que su dispositivo móvil esté conectado.

Ver precios en

OFERTA! BASCULA DIGITAL COMERCIAL. BALANZA PESA DIGITAL ELECTRONICA PARA COMERCIO. 30KG. - GSH

Ver precios en

Calculadoras científicas

Casio FX-82MS-2-S-ET-B, Calculadora Científica, 1, Gris Oscuro

• Gran botón de cursor para navegar, recuperar y editar cálculos; cómodo sistema de menús para cálculos estadísticos
• Pantalla de clara disposición como, p; ej., símbolo de separación de millares, indicación exponencial como símbolo x10, mayor presentación de la línea superior, etc
• 1 memoria de medias, 8 memorias de constantes, Función SCI/FIX/ENG, Cálculo de porcentajes, 24 niveles de paréntesis
• Funciones de trigonometría, Conversión de coordenadas polares en coordenadas rectangulares y viceversa, Funciones hiperbólicas e hiperbólicas inversas
• Cálculos en grado centesimal, grado sexagesimal y medida de arco, transformación de sexagesimal a decimal y viceversa, sistema automático de cálculo de fracciones

Ver precios en

Casio FX-85SPXII Iberia- Calculadora científica, Recomendada para el curriculum español y portugués, 252 funciones, solar, color azul

• Calculadora científica con menú y instrucciones en tu idioma: Castellano, catalán, euskera y portugués
• Idiomas: Castellano, Catalán, Portugués y Euskera
• Tiene 274 funciones, menú de iconos, repetición múltiple, 24 niveles de paréntesis, memorización de variables
• Funciones trigonométricas y funciones trigonométricas inversas, funciones hiperbólicas e hiperbólicas inversas, cálculo de potencias y raíces, cálculo logarítmico, cálculo exponencial
• Cálculo de raíces, combinatoria y permutación, factorización de números primos, generación de números enteros aleatorios, fracciones conversión de sexagesimal a decimal y viceversa, cálculos de grados

Ver precios en

Helect H-1002- Calculadora Científica, 2 Líneas Muestran, Gris

• La calculadora científica profesional tiene 240 funciones científicas. Permite procesar fácilmente cálculos estadísticos variables de 1 y 2, tres modos de ángulo (grados, radianes y graduados) y modos de notación científica y técnica
• Pantalla panorámica HD de 12 dígitos. La pantalla de 2 líneas muestra entradas y resultados simultáneamente. Funciona de manera eficiente y no comete errores
• Diseño ergonómico y proporciona un agarre cómodo. Botones atractivos, números claros y resistentes a los arañazos
• Una robusta caja de protección deslizante cubre ambos lados de la calculadora. Proteger botones y cuerpo del dispositivo
• El paquete incluye: 1 calculadora científica, instrucciones (idioma español no garantizado)

Ver precios en

Casio FX-82SP CW - Calculadora Científica, Recomendada para el Curriculum Español y Portugués, 5 Idiomas, más de 300 Funciones, Color Gris Oscuro

• Escritura natural, pantalla de 4 a 6 líneas de alta resolución
• Más de 300 funciones; simplificación de fracciones, factorización en números primos, MCM y MCD
• Funciones trigonométricas, hiperbólicas, exponenciales y logarítmicas; estadística
• Código QR; menú MathBox

Ver precios en

Instrumentos de medición

Mitutoyo 2046S - Herramienta de medición y distribución (tamaño: 0.01x10mm)

• La abrazadera del bisel y la palanca de elevación (opcional) se pueden colocar en el lado derecho o izquierdo.Se pueden instalar y quitar fácilmente sin herramientas.
• FALSO a través de los orificios para tornillos en el marco y la adhesión segura entre el bisel y el cristal, así como el uso de una junta tórica evita la penetración de agua o aceite.Precisión: 13 µm / Graduación: 0,01 mm / Calibrado: FALSO / Lectura del cuadrante: 0-100 (100-0)
• Asegúrese de comprar un producto Mitutoyo original.Este instrumento es suministrado por Mitutoyo UK.Comprar de nosotros significa comprar instrumentos Mitutoyo originales directamente del fabricante premium de JPese con la calidad, durabilidad y precisión excepcionales que usted espera legítimamente.
• Vástago de acero inoxidable
• Oreja trasera
• Eje de acero endurecido
• Cristal con revestimiento duro para resistencia a los arañazos
• Resistencia mejorada al polvoy agua

Ver precios en

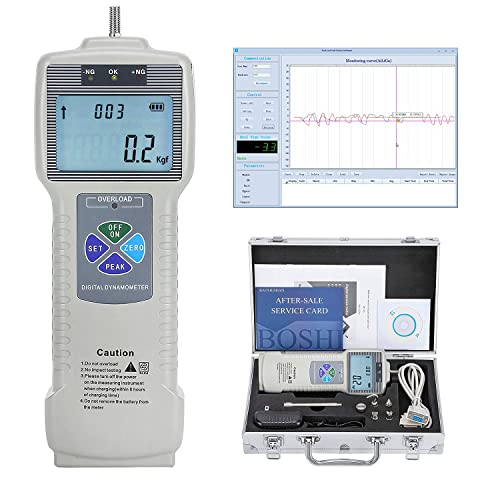
BAOSHISHAN Medidor de fuerza digital Probador de dispositivo de medición push-pull con interfaz USB-RS232 Instrumentos de medición de fuerza LCD (1000N)

• Unidad de [parámetro]: kgf / lbf / N conmutación de tres unidades | Resolución: 0,1 N | Pantalla LCD de 5 dígitos | Precisión: ± 0,2% | Dimensión: 220 * 78 * 32 mm | Peso neto: 520 g.
• [Fácil de llevar] Portátil con estuche de transporte. Completos accesorios para cumplir con los requisitos de medición y tornillos para montaje en banco de pruebas. [Tenga en cuenta que el dispositivo de medición de fuerza ZP solo es adecuado para bancos de pruebas APW (ASIN: B07Z1BRHGL) y bancos de pruebas APH (ASIN: B07YWYSBWP).].
• [Visualización de cambio de pantalla] Cuando el medidor de fuerza se voltea para su uso, la visualización de la pantalla se puede voltear al mismo tiempo configurando (presione ENVIAR repetidamente), lo cual es conveniente para leer datos. Repita el mismo proceso para retroceder la pantalla. Medición inmediata y de precisión --- Sensor incorporado de alta sensibilidad, velocidad de medición rápida y alta precisión.
• [Almacenamiento de fecha] Los datos se pueden guardar para verlos fácilmente o exportarlos para su análisis. Con la interfaz USB y RS232, la función de almacenamiento de datos puede almacenar 128 bits de datos. Puntos de viñeta. 3 unidades intercambiables: admite visualización de tres unidades diferentes: Lb, Kg, N, interruptor de un botón, fácil de usar.
• [Batería] Batería incorporada de gran capacidad. Duración de la batería: ≥ 300 veces. El voltaje de carga está entre 100 V y 240 V. El tiempo de carga no debe exceder las 8 horas.

Ver precios en

Instrumento de medición de ruido Medidor de sonido de decibelios digital Medidor de temperatura Medidor de humedad Detector 3 en 1 Probador de pantalla grande montado en la pared interior

• Función de calibración automática.
• El brillo de la pantalla se puede ajustar a mano.
• Diferentes colores y expresiones faciales muestran la calidad del entorno, muy realista.
• Puedes ponerlo sobre la mesa o colgarlo en la pared.
• Pantalla grande para facilitar la lectura.

Ver precios en

Newaner Calibre Digital, Pie de Rey de Fibra de Carbono de 150 mm / 6 " con Pantalla LCD Transparente y Batería de Respaldo, Calibre para Mediciones Externas, Internas, de Profundidad y de Paso

• 【Calibrador Digital Profesional】El pie de rey digital ha pasado nuestras rigurosas pruebas para garantizar una precisión más precisa. El rango de medición de los pie de rey digital es de 0 a 6 "/ 150 mm, lo que es muy adecuado para uso en el hogar, la escuela, el taller y la fábrica.
• 【Función Cero】El calibre digital profesional ​tiene un botón CERO, podemos restablecer el valor de medición, lo que hace que la operación de medición sea más flexible.
• 【Gran Pantalla LCD】Pantalla LCD grande y fácil de leer, la lectura se puede mostrar en formato de pulgadas o milímetros, la lectura es más clara, muy adecuada para personas con baja visión. Cuando no ha utilizado la calibrador digital mucho tiempo, la pcalibrador digitalse apagará automáticamente.
• 【Ligero y Portátil】La calibrador está hecha de material compuesto de fibra de carbono, que es más ligero y seguro que el acero inoxidable.
• 【Lo Que Puedes Conseguir】Calibre* 1, batería * 2 (el calibre puede durar más), caja de plástico * 1 (conveniente para almacenar y proteger el calibre)

Ver precios en